|
|
LES PROPRIÉTÉS ÉLECTRIQUES DE LA MEMBRANE NEURONALE
|
| La membrane neuronale est constituée d'une bicouche lipidique dans laquelle s'insèrent des protéines. Elle sépare le compartiment intracellulaire du compartiment extracellulaire. |
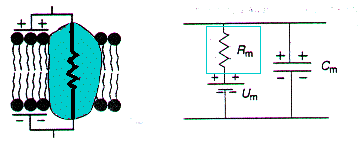 |
|
Les protéines membranaires sont des molécules chargées électriquement et, comme tout élément porteur de charges, peuvent conduire un courant électrique. Cette propriété peut être schématisée par une conductance ou par une opposition au passage du courant, soit par une résistance (inverse de la conductance : R = 1/g). membranaire transversale. Le circuit électrique équivalent à la membrane neuronale correspond donc jusque là à celui d'un générateur de courant (pile) de 60 mV dont le pôle positif est orienté vers le compartiment extracellulaire et le pôle négatif vers l'intérieur de la cellule alimentant une résistance membranaire Rm. La valeur de cette résistance membranaire (Rm), directement fonction de la quantité de protéines incluses dans une portion de membrane, est très variable : de 102 à 104 W . cm2; ces valeurs correspondent à des conductances (g = 1/R) variant de 10-4 à 10-2 Siemens / cm2.
À l'inverse, la bicouche lipidique est constituée de phospholipides non conducteurs, donnant à la membrane des propriétés capacitives, qui peuvent être représentées par un condensateur (deux éléments conducteurs séparés par un isolant) de capacité Cm. Ce condensateur ne modifie pas la valeur de la ddp mais joue le rôle d'un "réservoir" de charges, qui absorbe les variations instantanées de ddp entre les deux faces de la membrane. La séparation des charges positives et négatives portées par le condensateur induit une ddp entre les deux éléments conducteurs telle que V (Volts) = Q (Coulombs) / Cm (Farads) où Q est la charge portée par les éléments conducteurs. La valeur de la capacité membranaire Cm varie peu d'un élément de membrane à l'autre; elle est en moyenne de 1 µF/cm2.
|
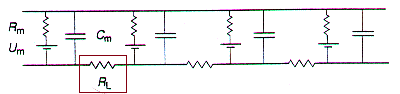 |
|
Les deux milieux, intra- et extracellulaire, ne sont pas des conducteurs parfaits. Ils présentent une résistance vis à vis du passage du courant électrique, qui peut être schématisée par une résistance longitudinale RL. Le schéma du circuit électrique équivalent à la membrane neuronale est maintenant quasi complet.
|
| Ces
propriétés électriques de la membrane neuronale
ont des conséquences fonctionnelles.
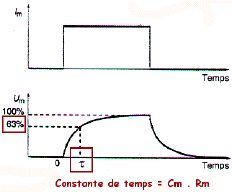
Si l'on tient compte des propriétés résistives de la membrane neuronale (résistance transversale Rm), l'injection d'un courant I au travers de cette membrane (courant transmembranaire Im) fait apparaître, aux bornes de cette membrane, une tension Um telle que :
En réalité, si la variation du courant est rapide, la variation du potentiel de membrane suit une courbe exponentielle, du fait des propriétés capacitives (Cm) de la membrane. La résistance transversale Rm et la capacité Cm conjuguent leurs effets pour déterminer l'évolution dans le temps de l'installation de la tension Um aux bornes de la membrane. Le produit Rm . Cm est la constante de temps du circuit (t). Ce produit indique, en secondes, le temps nécessaire pour que la tension aux bornes de la membrane atteigne 63,2% de sa valeur maximum.
|
 |
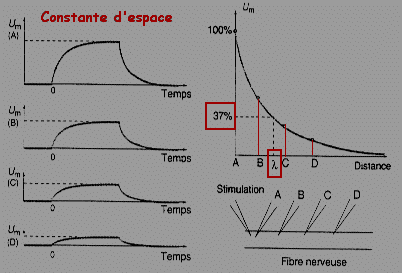
| Si l'on
applique un courant très près d'un point A de la
membrane d'un axone et que l'on mesure la tension obtenue aux
points A, B, C et D, de plus en plus éloignés du
point d'application, on observe que l'amplitude de la tension
maximum observée va en diminuant de A à D. Ce phénomène
est dû à la résistance longitudinale (RL)
de la fibre nerveuse. Le courant qui traverse la résistance RL de chaque segment (A-B / B-C / C-D) provoque une chute de tension égale au produit de ce courant par la résistance RL du segment. Si l'on représente l'évolution des tensions maximales mesurées aux différents points A, B, C et D en fonction de leur distance par rapport au point de stimulation, on observe que la chute de tension suit une courbe exponentielle. La distance correspondant à une baisse de la tension de départ de 63,2% détermine la constance d'espace du système (l). |
 |
| Or, la
chute de tension au travers de RL est directement proportionnelle
à la valeur même de RL. Ainsi, si la résistance longitudinale est faible, la chute de tension est faible et le signal peut être conduit sur une grande distance : la constance d'espace l est élevée. Au contraire, si la résistance longitudinale est importante, la chute de tension est importante et le phénomène initial décroît très vite : la constance d'espace l est faible. La résistance longitudinale RL est directement liée au volume de l'axoplasme : une grande résistance longitudinale, et donc une constance d'espace faible, est due à un faible volume de l'axoplasme, qui correspond à un axone de faible diamètre; au contraire, une fibre de gros diamètre a un volume axoplasmique important, une résistance longitudinale RL faible et donc, une constance d'espace élevée. La propagation des phénomènes électriques le long des fibres nerveuses sera donc plus ou moins efficace selon le diamètre des fibres. |
 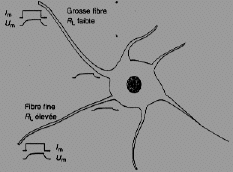 |
- Fibre de gros diamètre volume élevé RL basse <=> chute de tension basse => l élevée
- Fibre de petit diamètre faible volume RL élevée <=> chute de tension élevée => l
basse
|
| De par sa structure, la membrane neuronale est mauvaise conductrice. Une stimulation électrique de cette membrane est déformée comme dans un système résistif-capacitif (Rm - Cm) et ne se propage que sur de courtes distances liées aux diamètres des fibres (RL).
|
|
